物価上昇率が低い場合は実質賃金上昇率は名目賃金上昇率と物価上昇率の差で概算できる。概算だから正式な式で算出した数値との間に誤差が生じる。その誤差が最大でどのくらいになるのかグラフにすればイメージは掴めるが、実際の値が知りたければ数式があった方が良いので、導出してみた。
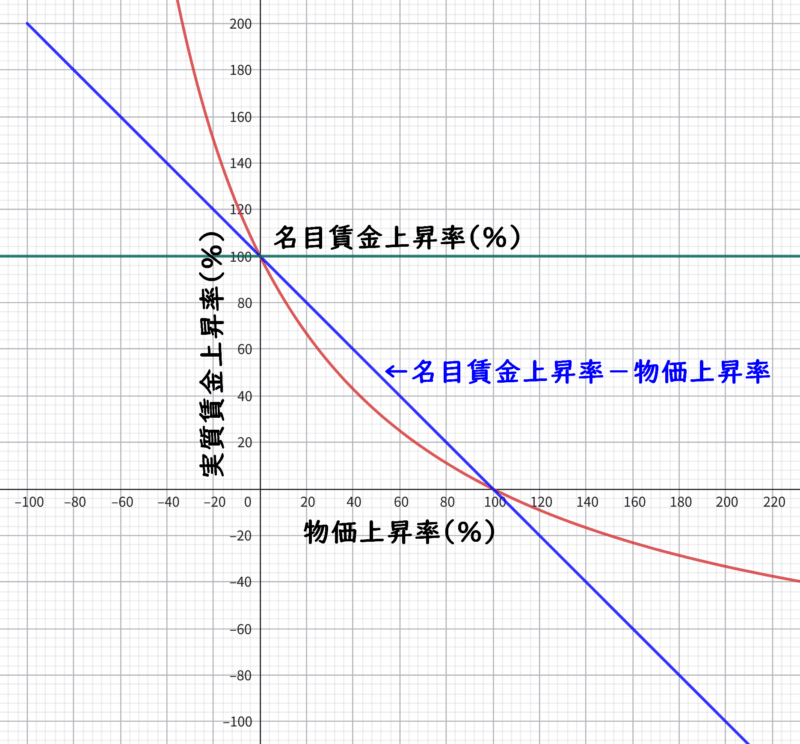
実質賃金上昇率を算出する数式と概算は次の通り。\eqref{eq:実質賃金上昇率} が正式な数式で、\eqref{eq:実質賃金上昇率の概算} が概算を求める式である。
\begin{empheq}[left=\empheqlbrace]{align}
実質賃金上昇率\,(\mathrm{\%})&=\frac{名目賃金上昇率\,(\mathrm{\%}) - 物価上昇率\,(\mathrm{\%})}{100+物価上昇率\,(\mathrm{\%})} \times 100 \label{eq:実質賃金上昇率} \\
実質賃金上昇率\,(\mathrm{\%})&=名目賃金上昇率\,(\mathrm{\%}) - 物価上昇率\,(\mathrm{\%}) \label{eq:実質賃金上昇率の概算}
\end{empheq}
正式な数式で実質賃金上昇率を算出した場合を $y_{精算}$ 、概算で算出した場合は $y_{概算}$ とし、名目賃金上昇率を定数の $a$ 、物価上昇率を変数の $x$ とすると、\eqref{eq:実質賃金上昇率} と \eqref{eq:実質賃金上昇率の概算} は次のようになる。
\begin{empheq}[left=\empheqlbrace]{align}
y_{精算}&=\frac{a - x}{100+x} \times 100 \label{eq:精算} \\
y_{概算}&=a - x \label{eq:概算}
\end{empheq}
ここで、物価の最小値は $0\,円$ なので、物価上昇率 $x$ の最小値は $-100\,(\mathrm{\%})$ であるから、ここでは $x \gt -100$ だけを考える。また、名目賃金の最小値も $0\,円$ なので、名目賃金上昇率 $a$ の最小値は $-100\,(\mathrm{\%})$ ( $a \gt -100$ )である。
調べたいのは $y_{精算}$ と $y_{概算}$ の差である。
\begin{equation}
D(x)=y_{概算}-y_{精算} \label{eq:誤差}
\end{equation}
\eqref{eq:精算} と \eqref{eq:概算} を \eqref{eq:誤差} に代入すると $D(x)$ は次のようになる。
\begin{equation}
D(x)=(a - x)-\frac{a - x}{100+x} \times 100 \label{eq:誤差代入}
\end{equation}
整理すると $D(x)$ は次のようになる。
\begin{equation}
D(x)=(a-x) \left( \frac{x}{100+x} \right)=\frac{ax - x^2}{100+x} \label{eq:誤差整理}
\end{equation}
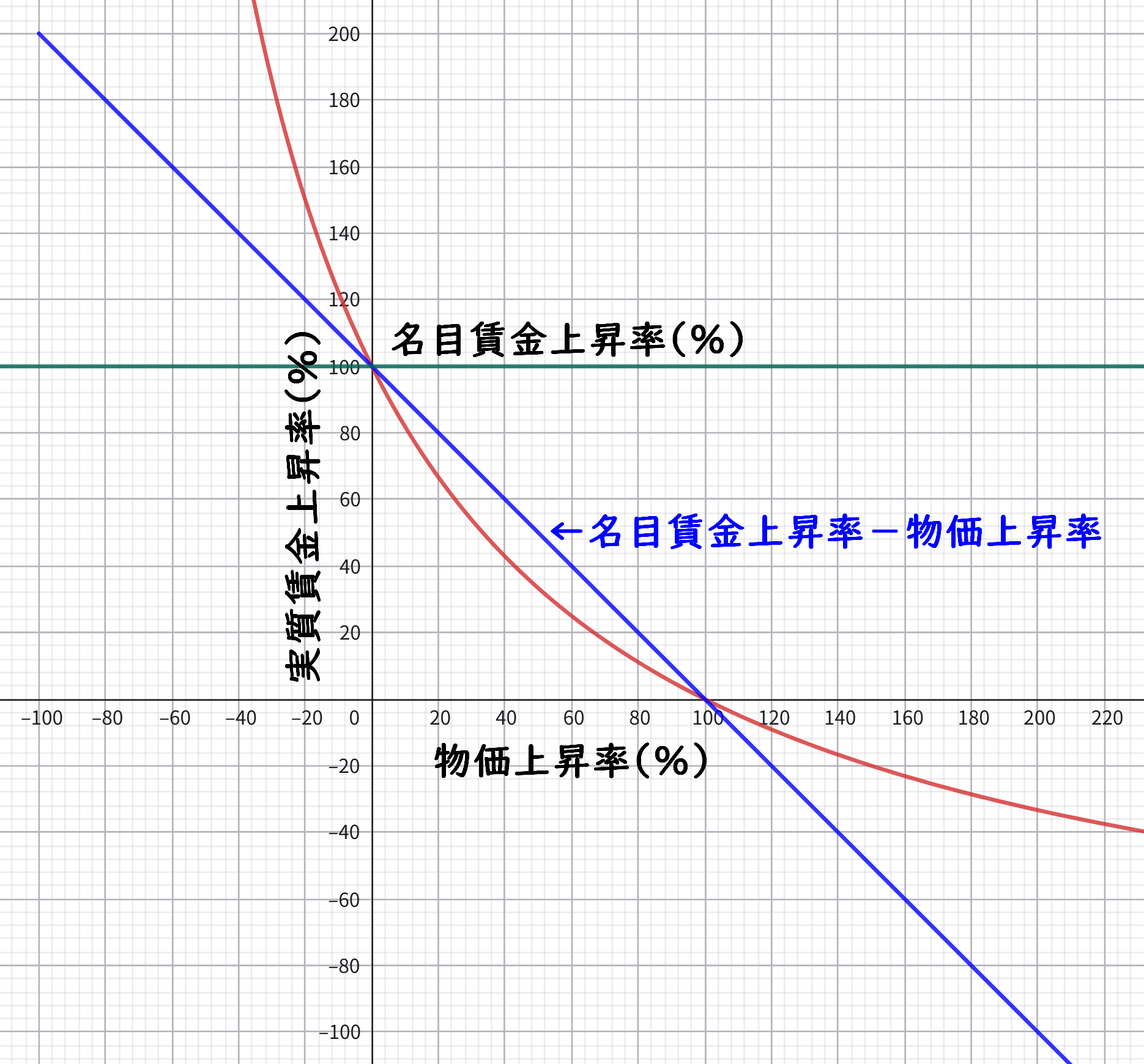
$x=0$ と $x=a$ で $D(x)=0$ となる( $y_{精算}$ と $y_{概算}$ の差が無くなる)ことが分かる。また、$x \gt -100$ なので、$D(x)$ の分母は常に正で、分子は上に凸の二次関数なので $-100 \lt x \lt 0$ と $x \gt a$ の範囲では $D(x)$ は負の値になる。すなわち、その範囲では、$y_{概算} \lt y_{精算}$ になる。$0 \lt x \lt a$ の範囲では、$D(x)$ は正の値になるが、上記のグラフを見ると、中央辺りで $y_{精算}$ と $y_{概算}$ の差が最大になっているように見える。知りたいのは、$0 \lt x \lt a$ の範囲で $D(x)$ が最大となる $x$ の値と、その時の $D(x)$ の値である。
$D(x)$ が最大となる $x$ を見つけるためには、$x$ について微分し、$D'(x)=0$ となる点を求める。
商の微分公式 $\left( \frac{f}{g} \right)' = \frac{f'g - fg'}{g^2}$ を用いる。$f(x) = ax - x^2$ とすると $f'(x) = a - 2x$、$g(x) = 100+x$ とすると $g'(x) = 1$ だから、$D'(x)$ は次のようになる。
\begin{align}
D'(x)
&= \frac{(a-2x)(100+x) - (ax-x^2)(1)}{(100+x)^2} \notag \\
&= \frac{-x^2 - 200x + 100a}{(100+x)^2} \label{eq:誤差微分}
\end{align}
$D'(x)$ の分母は常に正なので、$h(x) = -x^2 - 200x + 100a$ とすると $h(x) \gt 0$ で $D'(x) \gt 0$、$h(x) \lt 0$ で $D'(x) \lt 0$ になる。$h(x)$ は次のように変形できる。
\begin{align}
h(x)
&= -x^2 - 200x + 100a \notag \\
&= -(x+100)^2 + 10000 + 100a \label{eq:誤差微分の分子}
\end{align}
$h(x)$ は $x=-100$ を頂点とする上に凸の放物線であることが分かる。
$D'(x)=0$ となるのは $h(x)=0$ の時である。$h(x)=0$ となる $x$ は二次方程式の解の公式を使って求める。
\begin{align}
x
&= \frac{-(-200) \pm \sqrt{(-200)^2 - 4(-1)(100a)}}{2(-1)} \notag \\
&= \frac{-200 \pm \sqrt{40000 + 400a}}{2} \notag \\
&= \frac{-200 \pm \sqrt{400(100 + a)}}{2} \notag \\
&= \frac{-200 \pm 20\sqrt{100 + a}}{2} \notag \\
&= -100 \pm 10\sqrt{100 + a} \label{eq:解の公式で解く}
\end{align}
$x \gt -100$ なので、$h(x)=0$ となる $x$ は次の $x_p$ である。
\begin{equation}
x_p=-100 + 10\sqrt{100 + a} \label{eq:x_p}
\end{equation}
$h(x)$ は $x=-100$ を頂点とする上に凸の放物線なので、$-100 \lt x \lt x_p$ では $h(x) \gt 0$ となり、$x \gt x_p$ では $h(x) \lt 0$ になる。したがって、$-100 \lt x \lt x_p$ では $D'(x) \gt 0$ となり、$x \gt x_p$ では $D'(x) \lt 0$ になる。
$D'(x) \gt 0$ で $D(x)$ は増加し、$D'(x) \lt 0$ で $D(x)$ は減少するので、$D(x)$ は $x=x_p$ で最大の $D(x_p)$ になる。
\begin{equation}
D(x_p)=(a-x_p) \left( \frac{x_p}{100+x_p} \right)=\frac{ax_p - x_p^2}{100+x_p} \label{eq:D(x_p)}
\end{equation}
ここで、$h(x_p) = -{x_p}^2 - 200{x_p} + 100a = 0$ なので、$D(x_p)$ は簡単な式に整理できる。
\begin{align}
D(x_p)
&= \left(\frac{{x_p}^2 + 200{x_p}}{100}-x_p\right) \left( \frac{x_p}{100+x_p} \right) \notag \\
&= \left(\frac{{x_p}^2 + 200{x_p} - 100{x_p}}{100}\right) \left( \frac{x_p}{100+x_p} \right) \notag \\
&= \left(\frac{{x_p}^2 + 100{x_p}}{100}\right) \left( \frac{x_p}{100+x_p} \right) \notag \\
&= \left(\frac{{x_p}(x_p + 100)}{100}\right) \left( \frac{x_p}{100+x_p} \right) \notag \\
&= \frac{{x_p}^2}{100} \label{eq:D(x_p)整理}
\end{align}
さて、名目賃金上昇率が100%の場合( $a=100$ )、10%の場合( $a=10$ )、5%の場合( $a=5$ )の概算値 $y_{概算}$ と正式な数式で計算した値 $y_{精算}$ との差 $D(x)$ の最大値 $D(x_p)$ を計算すると、次のようになる。
名目賃金上昇率が100%の場合( $a=100$ )
\begin{empheq}[left=\empheqlbrace]{alignat}{2}
&x_p&=41.42135624\,(\mathrm{\%}) \notag \\
&D(x_p)\ &=17.15728753\,(\mathrm{\%}) \notag
\end{empheq}
名目賃金上昇率が10%の場合( $a=10$ )
\begin{empheq}[left=\empheqlbrace]{alignat}{2}
&x_p&=4.880884817\,(\mathrm{\%}) \notag \\
&D(x_p)\ &=0.238230366\,(\mathrm{\%}) \notag
\end{empheq}
名目賃金上昇率が5%の場合( $a=5$ )
\begin{empheq}[left=\empheqlbrace]{alignat}{2}
&x_p&=2.46950766\,(\mathrm{\%}) \notag \\
&D(x_p)\ &=0.06098468\,(\mathrm{\%}) \notag
\end{empheq}
名目賃金上昇率が5%以下の場合は、実質賃金上昇率は名目賃金上昇率と物価上昇率の差で概算しても誤差がほとんどないことが分かる。
ただし、名目賃金上昇率が5%の時に誤差が最大になるのは物価上昇率が2.4695%の場合で、実質賃金上昇率の概算は $5-2.4695=2.5305\,(\mathrm{\%}) $ になるが、正式な式で算出した場合は $2.4695\,(\mathrm{\%}) $ なので、小数点以下2桁までを使おうとすると、誤差が気になるかもしれない。



コメント