実質賃金の上昇率は実質賃金の上昇分を上昇前の実質賃金で割れば求められるが、名目賃金の上昇率と物価の上昇率からも求められるらしい。名目賃金上昇率と物価上昇率の差を実質上昇率にしたくなるが、実際の数式はそんなに単純ではない。インターネットで検索すれば数式は見つからが、本当にその数式で正しいか確認することにした。ちなみに、日本では「毎月勤労統計調査」が行われていて、「実質賃金の伸び率」は「各月の実質賃金指数」と「前年同月の実質賃金指数」から算定しているらしい。ここでも、上昇率は前年同月と比べる。
まず、実質賃金と実質賃金上昇率、名目賃金上昇率は次の式で表される。
\begin{equation}
実質賃金=\frac{名目賃金}{消費者物価指数} \times 100 \label{eq:実質賃金}
\end{equation}
\begin{equation}
実質賃金上昇率=\frac{調査月の実質賃金 - 前年同月の実質賃金}{前年同月の実質賃金} \label{eq:実質賃金上昇率の定義}
\end{equation}
\begin{equation}
名目賃金上昇率=\frac{調査月の名目賃金 - 前年同月の名目賃金}{前年同月の名目賃金} \label{eq:名目賃金上昇率の定義}
\end{equation}
物価の上昇率は消費者物価指数の上昇率で算出する。
\begin{equation}
物価上昇率=\frac{調査月の消費者物価指数 - 前年同月の消費者物価指数}{前年同月の消費者物価指数} \label{eq:物価上昇率の定義}
\end{equation}
さて、式 \eqref{eq:実質賃金上昇率の定義} は次のように変形できる。
\begin{equation}
実質賃金上昇率=\frac{調査月の実質賃金}{前年同月の実質賃金} - 1 =\frac{調査月の実質賃金指数}{前年同月の実質賃金指数} - 1 \label{eq:実質賃金上昇率の変形定義}
\end{equation}
実質賃金指数は次のように求められる。
\begin{equation}
実質賃金指数=\frac{名目賃金指数}{消費者物価指数} \times 100 \label{eq:実質賃金指数}
\end{equation}
また、式 \eqref{eq:名目賃金上昇率の定義} \eqref{eq:物価上昇率の定義} はそれぞれ式 \eqref{eq:名目賃金上昇率の変形定義} \eqref{eq:物価上昇率の変形定義} のように変形できる。
\begin{equation}
名目賃金上昇率=\frac{調査月の名目賃金}{前年同月の名目賃金} - 1 =\frac{調査月の名目賃金指数}{前年同月の名目賃金指数} - 1 \label{eq:名目賃金上昇率の変形定義}
\end{equation}
\begin{equation}
物価上昇率=\frac{調査月の消費者物価指数}{前年同月の消費者物価指数} - 1 \label{eq:物価上昇率の変形定義}
\end{equation}
したがって、式 \eqref{eq:実質賃金上昇率の変形定義} は次のように変形できる。
\begin{align}
実質賃金上昇率
&=\frac{\frac{調査月の名目賃金指数}{調査月の消費者物価指数}}{\frac{前年同月の名目賃金指数}{前年同月の消費者物価指数} } - 1 \notag \\
&=\frac{調査月の名目賃金指数}{前年同月の名目賃金指数} \times \frac{前年同月の消費者物価指数}{調査月の消費者物価指数} - 1 \notag \\
&=\frac{1+名目賃金上昇率}{1+物価上昇率} - 1 \notag \\
&=\frac{1+名目賃金上昇率}{1+物価上昇率} - \frac{1+物価上昇率}{1+物価上昇率} \notag \\
&=\frac{名目賃金上昇率 - 物価上昇率}{1+物価上昇率} \label{eq:実質賃金上昇率の変形1}
\end{align}
このように、実質賃金上昇率が実質賃金の上昇分を上昇前の実質賃金で割り算するだけでなく、名目賃金の上昇率と物価の上昇率からも算出できることが分かった。
ここで、これまでの式での「上昇率」が小数(比率)であって百分率(%)ではないことに注意する必要がある。百分率(%)の数値を小数(比率)にせずに実質賃金上昇率を算出したい場合は、式 \eqref{eq:実質賃金上昇率の変形1} の右辺の分子と分母の両方を100倍して、左辺と右辺の両方を100倍した次の式を使う。
\begin{equation}
実質賃金上昇率\,(\mathrm{\%})=\frac{名目賃金上昇率\,(\mathrm{\%}) - 物価上昇率\,(\mathrm{\%})}{100+物価上昇率\,(\mathrm{\%})} \times 100 \label{eq:実質賃金上昇率の変形2}
\end{equation}
さて、式 \eqref{eq:実質賃金上昇率の変形2} を見ても分かる通り、実質賃金上昇率は名目賃金上昇率と物価上昇率の差($名目賃金上昇率 - 物価上昇率$)で求められるわけではない。
名目賃金上昇率を100%にした場合の物価上昇率と実質賃金上昇率の関係をグラフにすると次のようになる。($名目賃金上昇率 - 物価上昇率$)と大きく異なることが分かる。
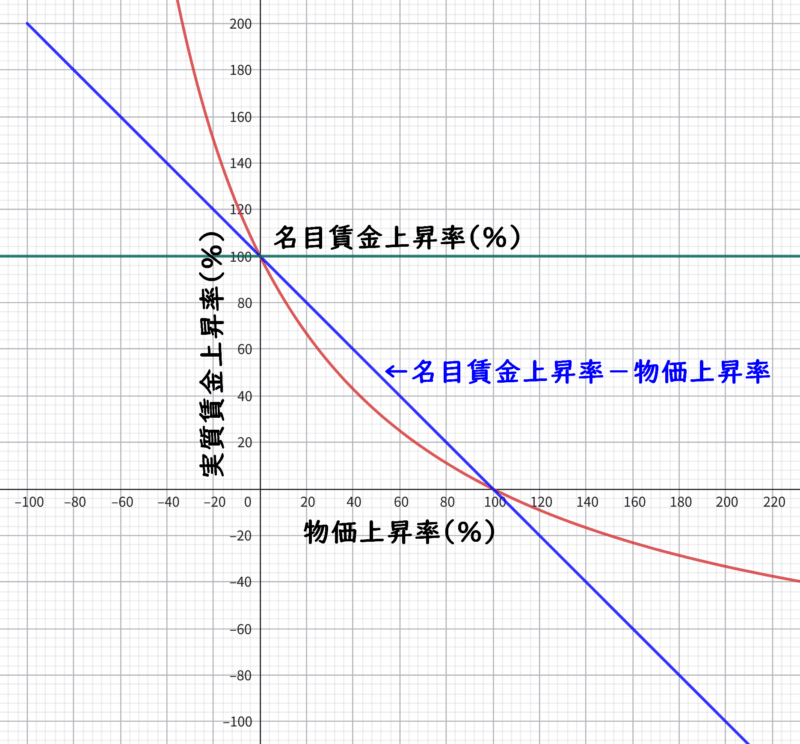
名目賃金上昇率が10%なら次のグラフのようになり、100%の時と比べて($名目賃金上昇率 - 物価上昇率$)に近くなる。
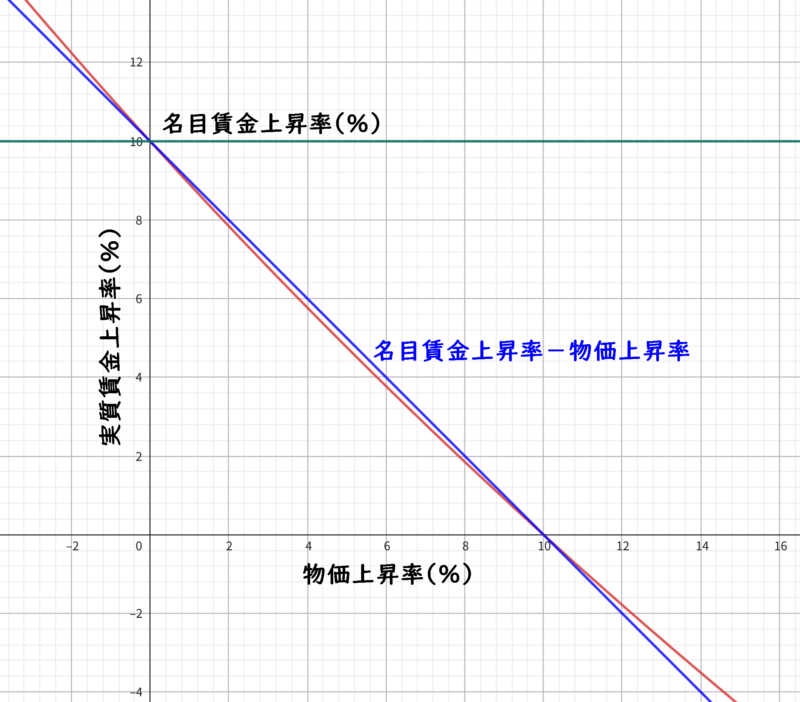
さらに、名目賃金上昇率が5%なら次のグラフのようになり、($名目賃金上昇率 - 物価上昇率$)で概算しても良さそうなほど近くなる。しかし、正確な数値を求めるのなら、式 \eqref{eq:実質賃金上昇率の変形1} や式 \eqref{eq:実質賃金上昇率の変形2} を使って算出した方が良い。
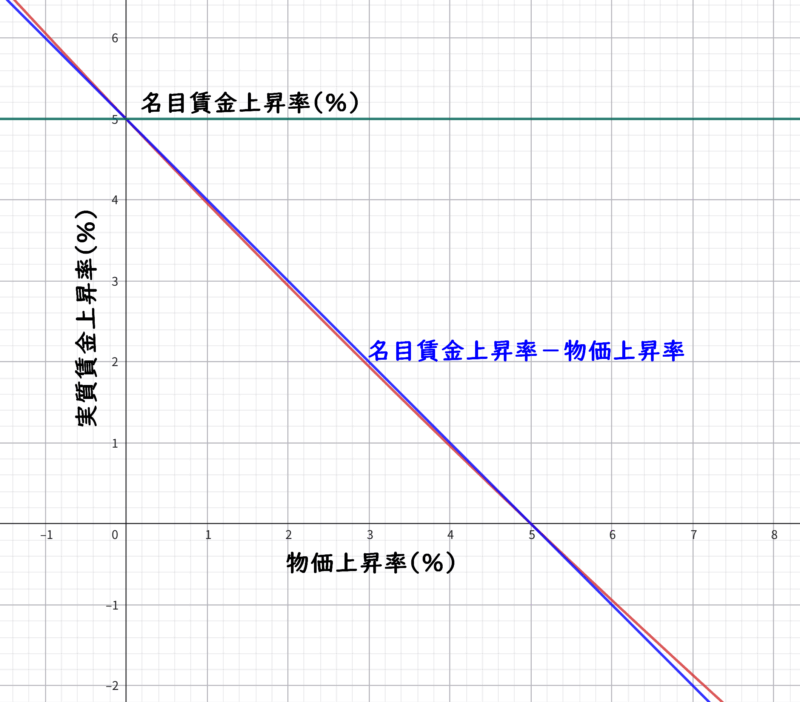
ちなみに、よほど特殊な状況でない限り物価が0円よりも低くなることは無いので、物価の上昇率が -1.0(-100%)よりも低くなることはないと考えて良い。したがって、式 \eqref{eq:実質賃金上昇率の変形1} や式 \eqref{eq:実質賃金上昇率の変形2} の分母は常にプラスなので、物価上昇率が名目賃金上昇率よりも高いと実質賃金上昇率がマイナスになる。




コメント